Simulation Tutorial (Gaussian data)
Source:vignettes/simulation_gaussian_data.Rmd
simulation_gaussian_data.RmdIn this tutorial, we’ll start by generating some simulated
spatio-temporal data, with the city of Bristol as our study region.
Next, we’ll walk you through the steps of running the Bayesian
Hierarchical Model (BHM) using the INLA-SPDE approach. Finally, we’ll
demonstrate the use the key functionality provided by the
fdmr package.
Data simulation
First we simulate some Gaussian distributed data observed at 55
spatial locations in Bristol, UK and across 6 time points. We use the
fdmr::retrieve_tutorial_data function and the
fdmr::load_tutorial_data function to retrieve and load in
the geographical information for the spatial locations in Bristol from
the fdmr example data store.
fdmr::retrieve_tutorial_data(dataset = "priors")##
## Tutorial data extracted to /home/runner/fdmr/tutorial_data/priors
sp_data <- fdmr::load_tutorial_data(dataset = "priors", filename = "spatial_dataBris.rds")Then we simulate the Gaussian data that exhibit spatio-temporal
correlation. These simulated data are finally organized into a data
frame named simdf, where each row corresponds to an
observation at a specific location and time. The variable
ID is the spatial location identifier. Variable
time denotes the time point. The variable datn
represents the simulated response data. The longitude and latitude
coordinates for each location are stored in the variables
LONG and LAT, respectively.
library(INLA)## Loading required package: Matrix## Loading required package: sp## This is INLA_24.06.27 built 2024-06-27 02:36:04 UTC.
## - See www.r-inla.org/contact-us for how to get help.
## - List available models/likelihoods/etc with inla.list.models()
## - Use inla.doc(<NAME>) to access documentation
n.time <- 6
n <- 55
locs <- as.matrix(sp_data@data[, c("LONG", "LAT")])
initial_range <- diff(range(locs[, 1])) / 3
max_edge <- initial_range / 2
mesh <- fmesher::fm_mesh_2d(
loc = locs,
max.edge = c(1, 2) * max_edge,
offset = c(initial_range, initial_range),
cutoff = max_edge / 7
)
spde <- INLA::inla.spde2.pcmatern(
mesh = mesh,
prior.range = c(initial_range, 0.5),
prior.sigma = c(1, 0.01)
)
sigma0 <- 7
range0 <- 0.03
kappa0 <- sqrt(8 / 1) / range0
tau0 <- 1 / (sqrt(4 * pi) * kappa0 * sigma0)
inla.seed <- sample.int(n = 1E4, size = n.time)
Q <- INLA::inla.spde.precision(spde, theta = c(log(tau0), log(kappa0)))
x.mat <- matrix(NA, ncol = n.time, nrow = mesh$n)
for (co in 1:ncol(x.mat)) {
x.mat[, co] <- INLA::inla.qsample(n = 1, Q)
}
A <- INLA::inla.spde.make.A(mesh = mesh, loc = locs)
x.dat <- matrix(NA, ncol = n.time, nrow = n)
for (t in 1:ncol(x.dat)) {
x.dat[, t] <- drop(A %*% x.mat[, t])
}
alpha <- 0.9
sp.mat <- matrix(NA, ncol = n.time, nrow = n)
sp.mat[, 1] <- x.dat[, 1]
for (t in 2:n.time) {
sp.mat[, t] <- alpha * sp.mat[, t - 1] + x.dat[, t]
}
beta0 <- 0.5
sigma_e <- 0.1
lin.pred <- beta0 + sp.mat
y.mat <- lin.pred + matrix(rnorm(n * n.time, 0, sigma_e), ncol = n.time)
simdf <- data.frame(
ID = rep(1:n, each = n.time),
time = rep(c(1:n.time), n),
datn = as.numeric(t(y.mat)),
LONG = rep(locs[, 1], each = n.time),
LAT = rep(locs[, 2], each = n.time)
)A histogram is created to visualize the distribution of the simulated Gaussian data.
hist(simdf$datn, main = "", xlab = "Data")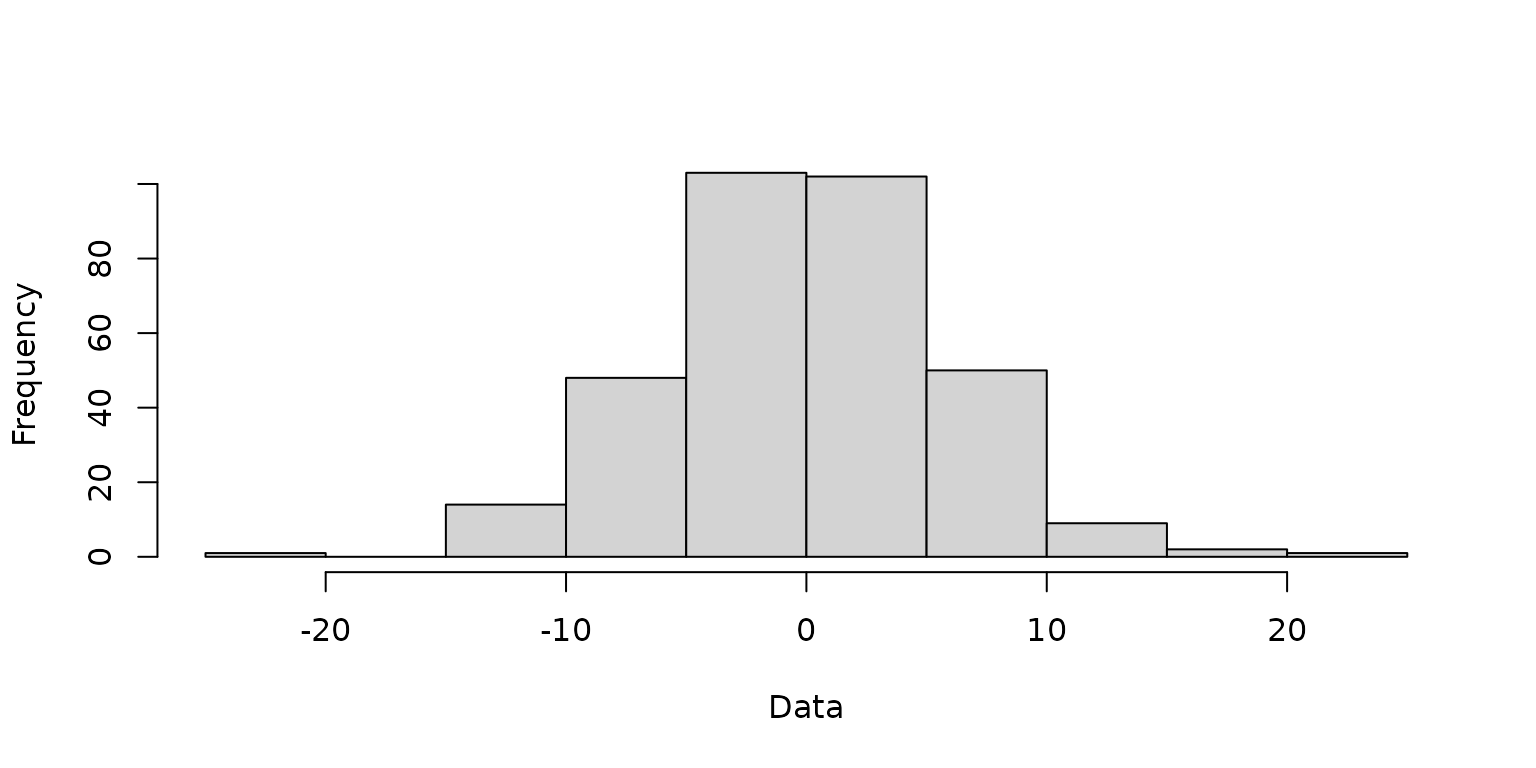
A histogram of the simulated Gaussian data.
We can also map the simulated data using the
fdmr::plot_map function. For example, a map of the
simulated data at the first time point is given as
fdmr::plot_map(
polygon_data = sp_data,
domain = simdf[simdf$time == 1, "datn"],
palette = "Reds",
legend_title = "Data",
add_scale_bar = TRUE,
polygon_fill_opacity = 1,
polygon_line_colour = "transparent"
)A map of the simulated data in Bristol at the first time point.
Model fitting
With the simulation dataset now prepared, our next step is to implement a Bayesian spatio-temporal model using the INLA-SPDE approach.
Generate mesh, build the SPDE model, and set priors for the spatial parameters
locs <- unique(simdf[, c("LONG", "LAT")])
initial_range <- diff(range(locs[, 1])) / 3
max_edge <- initial_range / 2
mesh <- fmesher::fm_mesh_2d(
loc = locs,
max.edge = c(1, 2) * max_edge,
offset = c(initial_range, initial_range),
cutoff = max_edge / 5
)
spde <- INLA::inla.spde2.pcmatern(
mesh = mesh,
prior.range = c(initial_range, 0.5),
prior.sigma = c(1, 0.01)
)Define how the process evolves over time, set prior for the temporal parameter and define a temporal index
rhoprior <- base::list(theta = list(prior = "pccor1", param = c(0, 0.9)))
group.index <- simdf$time
n_groups <- length(unique(simdf$time))We will use the function bru() of package
inlabru to fit the model. bru expects the
coordinates of the data, thus we transform simdf data set
to a SpatialPointsDataFrame using the function
coordinates() of the sp package.
sp::coordinates(simdf) <- c("LONG", "LAT")Fit the model
Finally, we fit the spatio-temporal model using SPDE approach and
AR(1) process by calling the function bru() of the package
inlabru.
Results summary
After completing the model fitting process, you can examine the main
result summaries by typing summary(inlabru_model).
Additionally, you can check the parameter estimates for fixed effects,
random effects, and hyperparameters as follows.
model_summary <- summary(inlabru_model)
model_fixed <- inlabru_model$summary.fixed
model_random <- inlabru_model$summary.random
model_hyperparams <- inlabru_model$summary.hyperparThe Deviance Information Criterion (DIC) value, which measures the goodness of model fit, can be examined as follows.
model_dic <- inlabru_model$dic$dicYou can obtain the model’s fitted values and compare them with the observed values as follows.
fitted_vals <- inlabru_model$summary.fitted.values[1:nrow(simdf), ]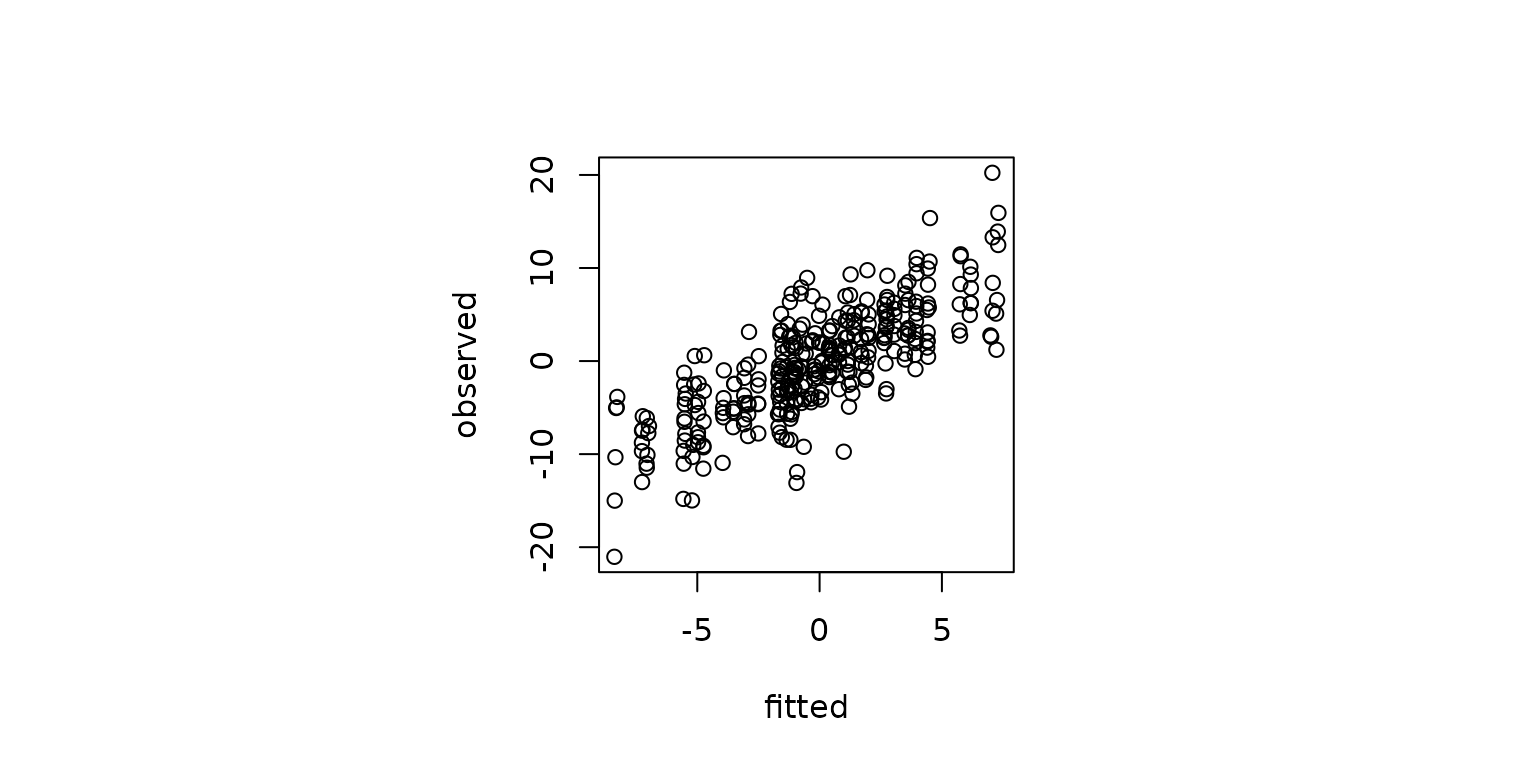
A plot of the fitted and observed values.
Exploring the functionality of the fdmr Package
Next, we’ll demonstrate the key functionality offered by the
fdmr package.
fdmr::plot_mesh
The fdmr::plot_mesh function displays both the mesh and
the observation points overlaid on the mesh.
fdmr::plot_mesh(mesh = mesh, spatial_data = simdf@coords)## Warning in fdmr::plot_mesh(mesh = mesh, spatial_data = simdf@coords): Cannot
## read CRS from mesh, assuming WGS84## Warning in fdmr::plot_mesh(mesh = mesh, spatial_data = simdf@coords):
## Attempting to convert to a data.frameA plot of the mesh.
fdmr::mesh_builder
fdmr provides an interactive mesh builder tool called
fdmr::mesh_builder. It allows you to build a mesh from some
spatial data, modify its parameters and plot it and the data on an
interactive map. To build a mesh, we need to pass sp_data
to the mesh_builder function.
fdmr::mesh_builder(spatial_data = sp_data)The interactive map allows you to customise the initial parameters
such as max_edge, offset and
cutoff to change the shape and size of the mesh.
Model builder Shiny app
fdmr provides a Priors Shiny app which allows you to
interactively set and see the model fitting results of different priors.
You can launch this app by passing the spatial and observation data to
the fdmr::model_builder function.
fdmr::model_builder(
spatial_data = sp_data,
measurement_data = simdf,
mesh = mesh,
time_variable = "time"
)fdmr::model_viewer
fdmr provides a separate Shiny app which allows you to
intuitively visualize the model output. You can launch this app by
passing the bru model object, the mesh, observation data
and data distribution as arguments to the
fdmr::model_viewer function.
fdmr::model_viewer(
model_output = inlabru_model,
mesh = mesh,
measurement_data = simdf,
data_distribution = "Gaussian"
)fdmr::plot_map
The fdmr::plot_map function generates a map of the
region based on the provided SpatialPolygonDataFrame.
fdmr::plot_map(polygon_data = sp_data)A map of the study region.